GRADO SEXTO


NÚMEROS ENTEROS
COMPARACIÓN DE NÚMEROS ENTEROS



DOCENTE: Giovanni Benavides G,
Mariela Coral, Teresa Erazo.
|
|||||||||||||||||||||||||||||||
AREA: Matemáticas
|
|||||||||||||||||||||||||||||||
FECHA DE APLICACIÓN:
|
20/04/2020 a 24/04/2020
|
||||||||||||||||||||||||||||||
GRADO:
|
6
|
||||||||||||||||||||||||||||||
ENTREGA DE ACTIVIDAD
|
La actividad se debe entregar el 24/04/2020
enviando la solución al correo del respectivo docente:
Giovanni
Benavides G apoyoacademicohgb@gmail.com
Teresa
Erazo teress_e@hotmail.com
Mariela
Coral Coralmariela11@gmail.com
|
||||||||||||||||||||||||||||||
ACTIVIDAD
Practica la representación en la recta numérica, valor
absoluto, y orden en los números enteros. Resuelve los siguientes puntos:
1. Escribe un número entero, que exprese la cantidad mencionada en
cada caso.
a) La cima de la montaña está a 568 m. de ALTURA
b) Pitágoras nació en el siglo VI a.C.
c) Un submarino está a 120 m. de PROFUNDIDAD
d) La temperatura de una ciudad es de 6°C BAJO CERO
e) Pablo CONSIGNÓ $ 500.000 en su cuenta
f) Sofía DEBE $ 450.000 al banco
2. Ubica los números enteros de cada grupo en la recta numérica
a) -5,4,7,0 b) -3,-2,-1,0 c) -8,2,0.1,6
3.
COMPLETAR
LA SIGUIENTE TABLA:
4.
Responde:
¿qué es el valor absoluto de un número entero? Escribir 2 ejemplos
5. Utilizando el concepto de valor absoluto
de un número entero solucionar los siguientes problemas:
a) Un vehículo sale del estacionamiento y
se desplaza 40 m. al norte. Luego, se devuelves sobre la misma calle y se
traslada 70m. hacia el sur y, finalmente, se mueve 20 m. hacia el sur.
¿cuántos metros recorrió en total el vehículo?
b) Un pájaro elevándose en el aire y un
buzo sumergido en el mar se encuentran a la misma distancia del nivel del
mar. ¿A qué altura se encuentra el pájaro y a qué profundidad el buzo, si los
separan 86m?
6.
En la
siguiente tabla se presentan los puntos de ebullición aproximados de algunos
elementos de la tabla periódica:
Teniendo en cuenta la tabla anterior, responder lo
siguiente:
a)
¿Cuál
es el elemento químico con mayor punto de ebullición?
b)
¿Cuál
es el elemento químico con menor punto de ebullición?
c)
Ordena
de menor a mayor los puntos de ebullición
|
|||||||||||||||||||||||||||||||

ADICIÓN DE NÚMEROS ENTEROS

SITUACIÓN PROBLEMA
a) Tenía
$ 200, mi papá me regaló $300. ¿cuánto dinero tengo en total?
b)
Debido
a la cuarentena, mi papá quedó sin trabajo y por consiguiente, no hubo el
dinero necesario para hacer unas compras prioritarias, por lo que fui a la
tienda de una vecina a que me fiara un kilo de arroz de $3.800, un kilo de
azúcar de $ 3.300, ¿cuánto se le debe a la vecina?
Para resolver las dos situaciones anteriores, qué
operación harías?
Bueno, creo que todos acertaron, deben SUMAR.
a)
200
+ 300= 500 R/ En total tengo $500
b)
(-3.800)
+ (-3.300) = -7.100 R/ En total se
debe a la vecina $7.100
(Recordar que
cuando son deudas el signo de las cantidades en negativo)
En los dos problemas
anteriores, los números enteros tienen igual signo, en a) los dos números
enteros son POSITIVOS, en b) los dos números enteros son NEGATIVOS, por lo
tanto se puede concluir que: Para SUMAR DOS O MAS NÚMEROS ENTEROS DEL MISMO
SIGNO, se suman y se conserva el
signo que tengan los números.
Así
podemos enumerar muchos más ejemplos. Realicemos la siguiente actividad:

|
||||||||||||||||||



Paso 2:Realiza la multiplicación de los números como ya sabes. En este caso . Por lo tanto el resultado de la multiplicación de menos tres y cinco es menos quince: . Obtendrás el mismo resultado si primero multiplicas los números y luego usas la ley de los signos.
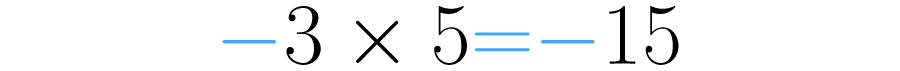
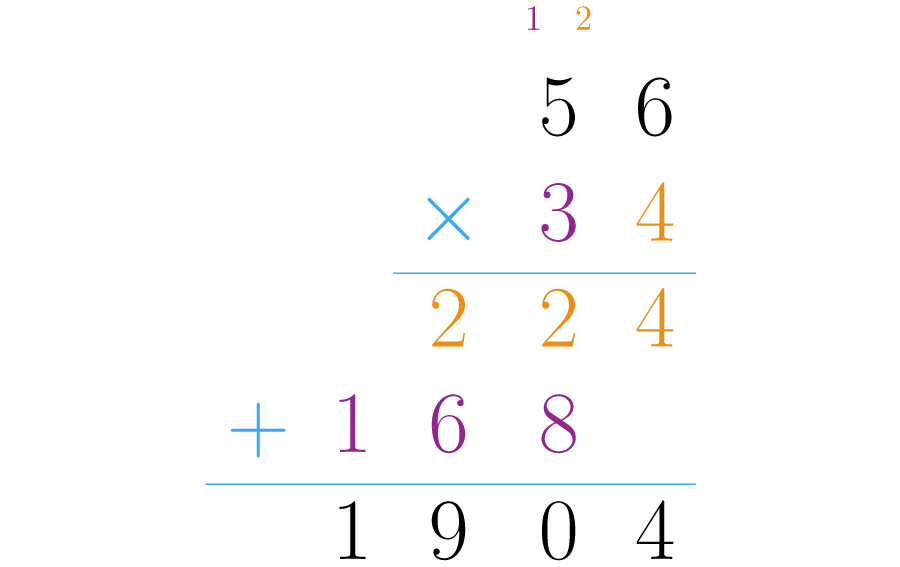

Ahora pensemos en la siguiente situación.

Podemos afirmar que entre todos le adeudan 2500 pesos a Cristina. Observa que el resultado fue un número negativo, esto quiere decir que se trata de una deuda.

No te olvides esta ley:

Realicemos la siguiente actividad:


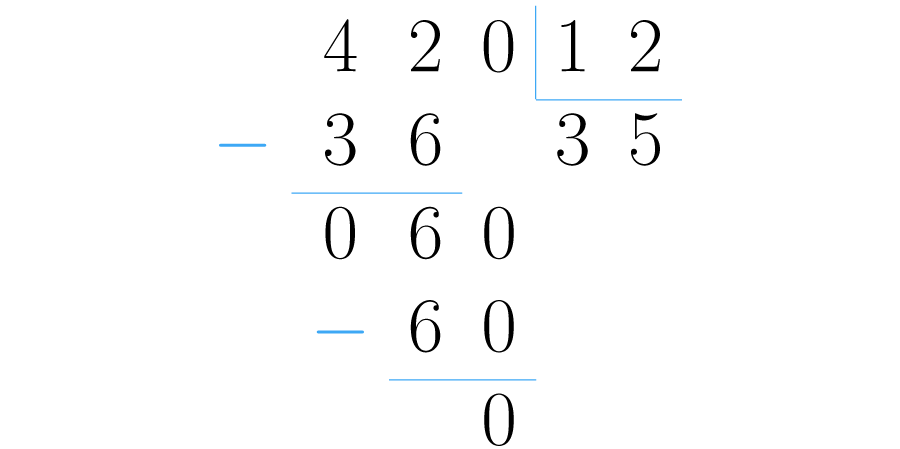
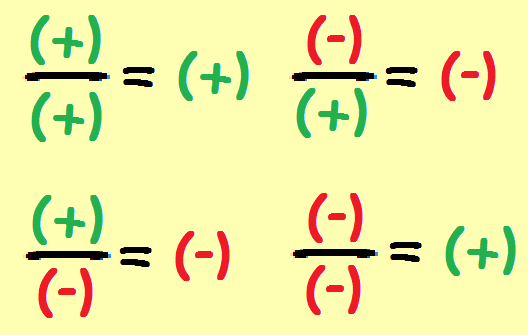
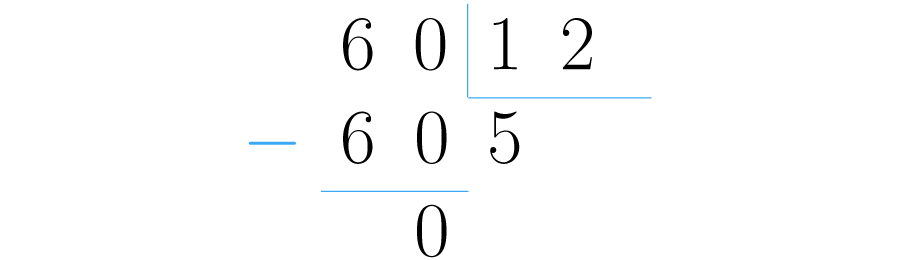

Si quieres aprender mas sobre la división de números enteros puedes mirar el siguiente vídeo.

DESCARGAR ACTIVIDAD DE DIVISIÓN
¿QUE TAN
IMPORTANTES SON LOS ANGULOS EN NUESTRA VIDA?
Hoy
en día podemos ver ángulos en casi cualquier parte de nuestro al rededor; por
ejemplo son usados para construir una casa como la que vemos en la siguiente
imagen
Importancia de los ángulos en la vida
cotidiana El estudio de los ángulos les permitió a los hombres abrirse paso en
el mundo, edificando ciudades, construyendo herramientas y confeccionando su
propia vestimenta. Todo esto a partir de la comprensión de importancia de aquel
pequeño punto en que se intersectan dos rectas.
El
100% de las cosas que rodean a la humanidad están hechas a partir de
conocimientos geométricos y trigonometría. Si bien es cierto que la gran
mayoría fueron automatizados por la industria y la tecnología, es bueno
comprender cuál es la base de todo.
Historia del conocimiento
angular El conocimiento geométrico documentado proviene de las impresionantes
civilizaciones egipcia y babilónica. No obstante, los griegos también se
adentraron en esta sorprendente rama de la matemática para poder desarrollar
sus maravillosas obras clásicas. De igual forma, estos grupos de hombres
exploraron con estas herramientas los cielos descifrando la relación existente
entre los 360 grados de una circunferencia y la duración de un año.
A
partir de estos primeros ensayos la humanidad comprendió los principios básicos
de la construcción y la albañilería. Con el paso del tiempo también aprendió a
construir proyectiles basados en conocimientos geométricos.
Creación
de la rueda
Siendo
la inversión más importante de todos los tiempos, este instrumento celestial
cambió el rumbo de la historia. Estudios afirman que el ejemplar más antiguo
data del año 3500, 3600 antes de cristo y que fue elaborada por una
civilización conocida como “Los Sumarios”.
Aprecia tus orígenes…
Si bien
es cierto que muchas personas no disfrutan los arduos conocimientos matemáticos
presentes en el entendimiento de las construcciones geométricas. Es importante
recalcar cuál es y cuál fue la importancia de los mismos para el origen y el
desarrollo de los hombres. Si no hubiera sido por estos conocimientos la
humanidad no hubiera avanzado tanto, en tampoco tiempo. Quizá ni siquiera sería
la especie dominante sobre la faz de la tierra.
A partir de la información anterior contesta las siguientes preguntas:
- ¿Qué tipos de figuras
geométricas observas en la fachada de la vivienda?
- ¿En qué partes de la
vivienda puedes observar ángulos?
- ¿Crees que hay
diferentes tipos de ángulos?
MEDICIONES Y
CLASIFICACION DE ANGULOS
¿PORQUÉ SON IMPORTANTES LOS ÁNGULOS EN LA
COTIDIANIDAD?
Los
ángulos son importantes ya que en nuestra vida cotidiana los utilizamos en
distintos sectores de cada trabajo, debemos pensar que serán utilizados de una
forma u otra; de manera que le den total perfección en la terminación de cada
labor realizada desde lo más simple hasta lo más complejo teniendo en cuenta su
buen funcionamiento.
Los ángulos son empleados en cada actividad que realizamos aunque no nos demos cuenta, desde cosas tan simples como cambiar un bombillo en donde se debe saber el ángulo perfecto como insertarlo debidamente hasta cosas más complicadas como la elaboración de unos planos en la construcción de un edificio.
Para actividades más complicadas también se
utilizan los ángulos, por ejemplo, cuando un arquitecto está elaborando los
planos de una casa necesita medir los ángulos para saber si cada puerta o
ventana va abrir correctamente o si va a quedar mal instalada por una medición
de un ángulo mayor o menor del necesario. Existen situaciones en las que pasa
desapercibida la importancia de los ángulos como en un partido de fútbol cuando
se va a realizar un pase o un penal y el jugador debe calcular con exactitud el
ángulo en el cual va a patear el balón para que sea una jugada exitosa. Por
estas y un sinfín de razones los ángulos son de suma importancia y lograr
conocerlos e incorporarlos en nuestra vida cotidiana solucionara más de algún
problema que se nos presente en un futuro próximo.
Para ayudarte a contestar las anteriores
preguntas es necesario conocer algunos conceptos de geometría y en especial la
teoría de ángulos y la forma como estos se clasifican.
¿Qué es
un ángulo?
Un
ángulo es la unión de dos o más rectas, segmentos o rayos que
tienen el mismo origen. (Vértice).
Los ángulos se miden en grados ° (grados),
por ejemplo:
Partes de un ángulo
El vértice de un ángulo
Se conoce por el nombre de
“vértice” a aquel lugar exacto en el que se intersectan las rectas o
semirrectas que conforman uno o más ángulos. También se le llama “vértice” al
punto en el que choca cualquier tipo de línea, es decir, es el lugar en el que
se cruzan dos circunferencias, cuadrados, rectángulos, rombos; cualquier tipo
de figura construida a partir de líneas.
¿Cómo se clasifican los ángulos?
Tipos
de ángulos de acuerdo a su medida:
·
Ángulos agudos: Mide entre
0° y 90°
Un ángulo
agudo lo podemos observar en el balcón de alguna casa, ya
que este ángulo está formado por dos semirrectas entre 0° y 90°
·
Ángulos rectos: Mide
90°
En nuestro
entorno un ángulo recto lo podemos observar en una ventana, paredes, sillas, en
una mesa, en el refrigerador, en la computadora, etc.
·
Ángulos obtusos:
Mide entre 90° y 180°
Un ángulo
obtuso lo podemos hallar en un poste de luz común, en
sillas o sillones reclinables, etc.
·
Ángulos llanos o colineales: Mide
180°
Un ángulo
llano lo podemos ver en un sube y baja de algún parque.
·
Angulo cóncavo o entrante: Mide
entre 180° y 360°
Lo
podemos observar en unas escaleras.
·
Ángulos perigonales: Mide
360°
Un ángulo
perigonal lo podemos observar en las llantas de un auto, un aro, un plato, un
vaso, un sartén, etc.
Tipos
de ángulos de acuerdo a sus lados con otro ángulo:
·
Adyacentes: Ángulos en
el mismo plano tienen un vértice y un lado en común.
·
Ángulos opuestos
al vértice: 2 rectas se cortan y
hacen ángulos opuestos por el vértice. Lo podemos observar en
la rejas rombo que encierran nuestras casas o parques, etc.
Tipos de ángulos de acuerdo a la suma
de sus medidas:
·
Ángulos complementarios:
2 o más ángulos que la
suma de 90°
Lo podemos observar en una clase
de educación física, cuando hacemos aperturas de piernas.
·
Ángulos
suplementarios: 2 o
más ángulos que la suma de 180°
Lo
podemos observar en una mesa donde comemos o hacemos tarea, porque la mesa
forma 2 ángulos de 90°.
·
Ángulos
conjugados: 2 o
más ángulos que la suma de 360°
Lo
podemos observar en un pastel partido por la mitad, o en más partes, etc.
Los ángulos los
utilizamos o vemos diariamente en nuestra vida cotidiana. Por ejemplo en
construcciones de casa, escaleras, en nuestros útiles escolares, en
nuestras casas, etc. En conclusión existen varios tipos de
ángulos y es necesario conocerlos ya que están presentes en nuestra vida
diaria. Los utilizamos todas las personas sin darnos cuenta de su importancia.
NOTA:
Un transportador es un instrumento que
mide ángulos en
grados y que viene en dos presentaciones básicas:
·
Transportador
con forma semicircular graduado en 180° grados. Es más común que el circular, pero
tiene la limitación de que al medir ángulos cóncavos (de más de 180° y menos de
360°), se tiene que realizar una doble medición.
·
Transportador
con forma circular graduado en 360° grados.
Por ejemplo, en la siguiente figura puedes ver como se mide el angujo A
obteniéndose un valor de 39 grados.

DESCARGAR ACTIVIDAD 6. CLASIFICACIÓN DE ÁNGULOS.


