GRADO DECIMO

  

FUNCIÓN MATEMÁTICA

Una función matemática es una relación que se establece entre dos conjuntos, a través de la cual a cada elemento del primer conjunto se le asigna un único elemento del segundo conjunto. Al conjunto inicial o conjunto de partida también se lo llama dominio; al conjunto final o conjunto de llegada se lo puede denominar codominio.

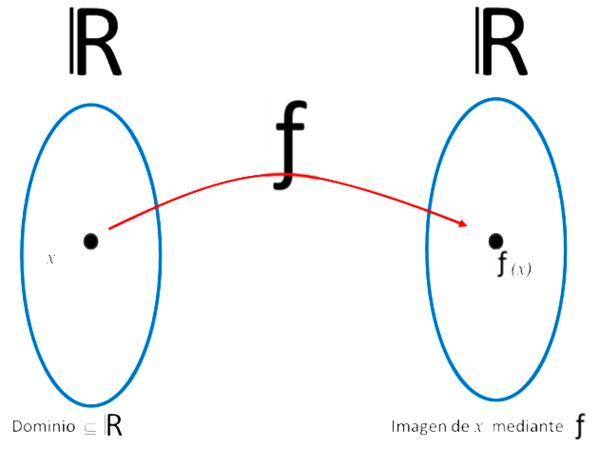
Por lo tanto, dados un conjunto A y un conjunto B, una función es la asociación que se produce cuando a cada elemento del conjunto A (el dominio) se la asigna un único elemento del conjunto B (el codominio). Aunque el codominio también recibe los nombres de imagen, rango o recorrido.

     Las funciones determinan las relaciones que existen entre distintas magnitudes tanto en Matemáticas, como en Física, Química, Medicina, Estadística, Economía, Ingeniería, Psicología... y permiten, entre otras muchas cosas, poder calcular los valores de cada una de ellas en función de otras de las que depende.

En la vida real hay muchos ejemplos de funciones que utilizamos diariamente entre ellos tenemos:
-       La relación de la cantidad de gasolina en galones y el kilometraje recorrido por un automóvil; vemos que entre más galones de combustible se recorrerá una mayor distancia en kilómetros.
-       En economía decimos que "el precio de una compra es directamente proporcional al número de unidades compradas de un cierto producto". Entre más artículo mayor es el costo.
-       El precio de la factura de la luz depende de una cantidad variable que es proporcional al consumo efectuado. En este caso, la relación entre el consumo efectuado y el coste de la factura viene dado por una funciones.
     
     Así podemos enumerar muchos más ejemplos.

ACTIVIDAD DE FUNCIONES
DOCENTE:  Giovanni Benavides G.
AREA: Matemáticas
FECHA DE    APLICACIÓN:	27/05/2020  a  01/05/2020
GRADO:	10-3
ENTREGA DE   ACTIVIDAD	La actividad se debe entregar el 01/05/2020 enviando la solución al correo: apoyoacademicohgb@gmail.com, whasapp.
ACTIVIDAD             Realiza la siguiente actividad que puedes encontrar en el siguiente enlace:               Actividad 1. Concepto de función.        Actividad 2. Responde las preguntas de competencias emocionales.        Actividad 3. Responde las preguntas de competencias ciudadanas.

                                                                   
                                                                                                                    ACTIVIDAD DE FUNCIONES

DOMINIO Y CODOMINIO DE UNA FUNCIÓN.

Al elemento genérico del dominio se lo conoce como variable independiente; al elemento genérico del codominio, como variable dependiente. Esto quiere decir que, en el marco de la función matemática, los elementos del codominio dependen de los elementos del dominio.

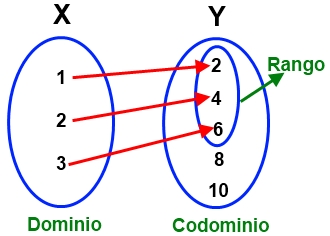
Hay distintas formas en que puede presentarse una función, mediante un enunciado, una tabla, una expresión algebraica o una gráfica, esta última es la que nos permite ver de un sólo vistazo su comportamiento global, de ahí su importancia.

Se relacionan así dos variables numéricas que suelen designarse con x e y. 

f: x → y=f(x) 

x -es la variable independiente. (Dominio)

y -es la variable dependiente. (Codominio, imagen, rango, recorrido)

En el siguiente vídeo se puede observar la relación de los elementos de un conjunto de partida y otro de llegada:

Por ejemplo, la función y = x² la podemos interpretar si pensamos en los números enteros donde entran los naturales del 1 al más infinito, además del 0 y los negativos hasta el menos infinito, podemos afirmar que a cada uno de ellos le corresponde solamente un cuadrado, que siempre es un número natural o cero: -3 al cuadrado es 9; 0 al cuadrado es 0; 7 al cuadrado es 49.

La función matemática ante la que nos encontramos en este caso tiene por un lado el conjunto de los números enteros (dominio) y por otro el de los naturales (codominio). Por lo general, denotamos una función indicando su nombre con minúscula seguido del nombre dela variable entre paréntesis y también en minúscula, que representa el elemento del dominio del cual queremos encontrar su imagen en el codominio. Si retomamos el ejemplo del párrafo anterior, podríamos decir que la función para hallar el cuadrado de un número entero dado es  y = x².

Pero que es el Dominio y recorrido de una función.

En el mundo de las matemáticas, es indispensable conocer el dominio  y el recorrido de una función. Por ello, vamos a hablar sobre el dominio de una función. Así mismo, indicaremos el término recorrido o imagen de una función solucionando ejemplos y ejercicios prácticos.

Dominio: se entiende por dominio de una función al conjunto de partida de la misma. Se trata del conjunto donde existe dicha función, es decir, el conjunto numérico que dicha función puede transformar. Matemáticamente, de denota al dominio de la siguiente manera:

Df = {R} cuando el dominio son los números reales (R).

Codominio o imagen: También se suele llamar Rango es el conjunto de llegada de la función. La función inicia en un conjunto que se transforma en el recorrido. Los resultados conforman un nuevo conjunto llamado codominio o imagen. Se trata del conjunto de valores que tiene la imagen al momento de la salida. Recordemos que:

• La variable X es un número real que pertenece al dominio de la función. Por ende, suele recibir el nombre de variable independiente.

• La variable y es también un número real, siendo llamada como “variable dependiente”. Su valor siempre se consigue aplicando la función F al valor de X. Por eso, siempre se suele denotar como: F(x) = y.

EJEMPLO 1:

Calcular el dominio, recorrido y gráfica de la función: 

f(x)=x2

Sea la función $f:R\to R$ dada por $f\left(x\right)=x^2$. Calculamos algunas imágenes remplazando los números reales en x.

• $f\left(0\right)=0^2=0$
• $f\left(1\right)=1^2=1$
• $f(-1)=(-1{)}^2=1$
• $f\left(2\right)=2^2=4$
• $f(-2)=(-2{)}^2=4$
• $f\left(3\right)=3^2=9$
• $f(-3)=(-3{)}^2=9$

ANALICEMOS:

Dominio:

El dominio de $f$ es el conjunto de los reales: $D\left(f\right)=R$.  (Los valores que puede tomar x)

Imagen: Im(f)

La imagen de $f$ es el conjunto de los reales no negativos, $\mathrm{Im(}f)=R^{+}$, porque el cuadrado de un número siempre es positivo.

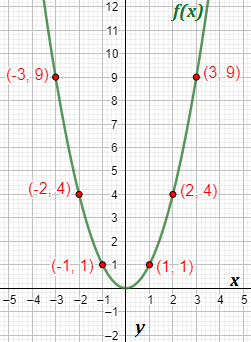
Gráfica.

La gráfica de la función $f$ es el conjunto de los puntos $(x,y)$ tal que $x$ es del dominio de la función $\mathrm{f\; y\; la\; variable\; "y"\; corresponde\; a\; f(x).\; Como\; se\; observa\; en\; la\; tabla:}$

f(x)=x2

x	F(x)
-3	9
-2	4
-1	1
0	0
1	1
2	4
3	9

Graficando en el plano cartesiano:

EJEMPLO 2:

Calcular el dominio, recorrido y gráfica de la función: 



Analicemos el Dominio:

Recordemos que una raíz cuadrada solo puede tomar valores positivos; ya que no existen raíces cuadradas de números negativos.

Por tanto, el dominio de la función sería los reales positivos. Df =  R+

Analicemos el Rango:

La raíz de un numero positivo siempre va a ser un numero positivo. Por tanto, el rango de la función raíz va a ser los reales positivos. Rf = R+

Realicemos la tabla de valores de x:

x	1	4	9	16
f(x)	1	2	3	4

En resumen podemos representar gráficamente el dominio y rango de la siguiente manera:

En el eje x el dominio.
En el eje y el Rango.

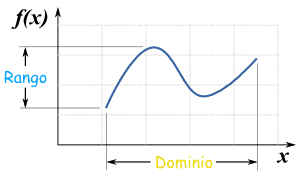
A continuación puedes observar un vídeo explicativo para identificar el dominio y recorrido de una función incluyendo los ejemplos vistos: 

EJERCICIOS EN CLASE: 

De acuerdo con el vídeo determina cual es el dominio y rango de las siguientes gráficas y envía las respuestas al grupo de whatsapp con tu nombre.

A)

B)

C)

ACTIVIDAD 2. DOMINIO Y RANGO DE UNA FUNCIÓN.

ACTIVIDAD 2. DOMINIO Y RANGO DE UNA FUNCIÓN
DOCENTE:  Giovanni Benavides G.
AREA: Matemáticas
FECHA DE APLICACIÓN:	06/05/2020  a  13/05/2020
GRADO:	10-3
ENTREGA DE ACTIVIDAD	La actividad se debe entregar el 13/05/2020 enviando la solución al correo: apoyoacademicohgb@gmail.com, whasapp.
NOTA: Colocar (nombre y apellidos; grado; número de lista) en todas y cada una las fotografías que se vayan a enviar por whasapp o por correo.

DESCARGAR ACTIVIDAD

COMO GRAFICAR FUNCIONES

Luego de ver la introducción a funciones,  vamos a revisar como graficar funciones básicas. El método que veremos es muy sencillo, y consiste en 3 pasos que revisaremos líneas abajo. Al final de este artículo, encontrarás un video con la gráfica de diferentes funciones que hemos preparado para practicar.

Pasos para graficar funciones básicas

1  Arma una tabla de valores, tabulando diferentes valores de “x”, “y”, y colocando los pares ordenados. Hagamos el ejemplo de la función:

 y = 2x + 1

x	-2	-1	0	+1	+2
y	-3	-1	+1	+3	+5
(x;y)	(-2 ; -3)	(-1 ; +1)	(0 ; +1)	(+1 ; +3)	(+2 ; +5)

2. Coloca los pares ordenados en el plano cartesiano.

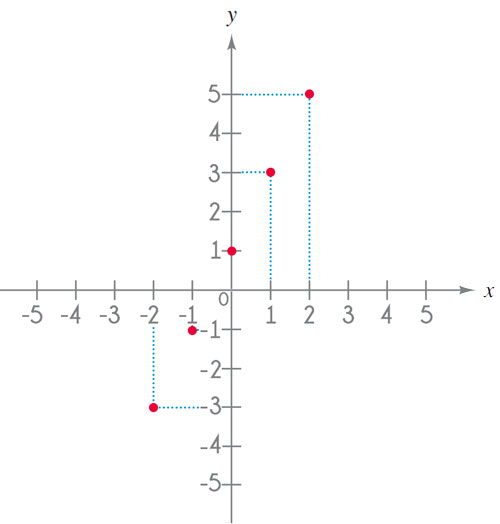
3. Une los puntos formando la curva.

Con estos pasos, puedes graficar cualquier función, ya sea lineal, cuadrática, exponencial, valor absoluto, entre otras. Más adelante, veremos otras funciones de mayor dificultad, analizando dominio, rango, intersecciones, paridad, asíntotas y más.

En los siguientes vídeos puedes ver como se grafican funciones:

Veamos como se hace una gráfica:

Ejemplo de función lineal:

Otro ejemplo de función lineal:

Tercer ejemplo en el siguiente vídeo:

Ahora podemos realizar la siguiente actividad.

ACTIVIDAD

ACTIVIDAD GRÁFICA DE FUNCIONES

TIPOS DE FUNCIONES

Recuerda que:

Las funciones matemáticas se definen como la expresión matemática de la relación existente entre dos variables o magnitudes. Dichas variables son simbolizadas a partir de las últimas letras del alfabeto, X e Y, y reciben respectivamente el nombre de dominio y codominio.

Dicha relación se expresa de tal modo que se busca la existencia de una igualdad entre ambos componentes analizados, y en general implica que para cada uno de los valores de X existe un único resultado de Y y viceversa (aunque existen clasificaciones de funciones que no cumplen con este requisito).

Asimismo, esta función permite la creación de una representación en forma de gráfica que a su vez permite la predicción del comportamiento de una de las variables a partir de la otra, así como posibles límites de esta relación o cambios de comportamiento de dicha variable.

Principales tipos de funciones matemáticas

A continuación os mostramos algunos de los principales tipos de funciones matemáticas, clasificadas en diferentes grupos según su comportamiento y el tipo de relación que se establece entre las variables X e Y. La función puede crecer o decrecer según el intervalo donde se analice.

Función polinómica

Una función polinómica f es una función cuya expresión es un polinomio tal como:

El dominio de las funciones polinómicas son todos los números reales.

Las funciones polinómicas son continuas en todo su dominio.

Función constante

Una función f es constante si la variable dependiente y toma el mismo valor a para cualquier elemento del dominio (variable independiente x).

En términos matemáticos, la función f es constante si para cualquier par de puntos x₁ y x₂ del dominio tales que x₁<x₂, se cumple que f(x₁) = f(x₂).

La gráfica de una función constante es una recta paralela al eje de abscisas X.

Función afín

Una función afín es una función polinómica de primer grado que no pasa por el origen de coordenadas, o sea, por el punto (0,0).

Las funciones afines son rectas definidas por la siguiente fórmula:

Los escalares m y n son diferentes de 0.

Función lineal

Una función lineal es una función polinómica de grado 1 que pasa por el origen de coordenadas, es decir, por el punto (0,0). Son funciones rectas de la forma:

También se llaman funciones de proporcionalidad directa. La constante m es la razón de proporcionalidad.

El término independiente n de la función afín es cero

Función identidad

Una función identidad es una función tal que la imagen de cualquier elemento es éste mismo:

Estas funciones también suele denotarse por id.

La función identidad es una función lineal de pendiente m = 1 que pasa por el origen de coordenadas, es decir, por el punto (0,0). Divide el primer y el tercer cuadrante en partes iguales, o sea, es su bisectriz.

Función cuadrática

Las funciones cuadráticas (o funciones de segundo grado) son funciones polinómicas de grado 2, es decir, el mayor exponente del polinomio es x elevado a 2 (x²):

Su representación gráfica es una parábola vertical.

Una función cuadrática puede tener dos raíces reales, una o ninguna. Las raíces de una función son los elementos del dominio que la hacen nula. Es decir, son los puntos donde la gráfica de la función corta al eje X

Función cúbica

Las funciones cúbicas (o funciones de tercer grado) son funciones polinómicas de grado 3, es decir, las que el mayor exponente del polinomio es x elevado a 3 (x³):

La representación gráfica de la función cúbica es:

Una función cúbica puede tener tres raíces reales dos o una. Las raíces de una función son los elementos del dominio que la hacen nula. Es decir, son los puntos donde la gráfica de la función corta al eje X.

Con lo aprendido podemos realizar la siguiente actividad.

DESCARGA LA ACTIVIDAD 4. TIPOS DE FUNCIONES.

Crecimiento y decrecimiento de funciones

Cuando se grafican las funciones se puede caer en tres casos:

·         Una función es decreciente en un intervalo (a,b) de su dominio para todo x1 y x2 que pertenece a ese intervalo donde se cumple que si x1 > x2, entonces f(x1) > f(x2). Es decir, la gráfica de la función al leerla de izquierda a derecha va de abajo hacia arriba.

·         Una función es creciente en un intervalo (a,b) de su dominio para todo x1 y x2 que pertenece a ese intervalo donde se cumple que si x1 < x2, entonces f(x1) < f(x2). Es decir, la gráfica de la función al leerla de izquierda a derecha va de arriba hacia abajo.

·         Una función es constante en un intervalo (a,b) de su dominio para todo x1 y x2 que pertenece a ese intervalo donde se cumple que para todo x1 y x2, entonces f(x1) = f(x2). Es decir, la gráfica de la función al leerla de izquierda a derecha queda totalmente horizontal.

Ejemplo: Analizar la siguiente gráfica de una función:

Continuidad de funciones

Intuitivamente una función f es continua si su gráfica no tiene interrupciones ni saltos, ni oscilaciones indefinidas, en el sentido que se puede dibujar sin levantar el lápiz de la hoja de papel.

Continuidad de una función de una variable real: Una función f de ℝ en ℝ es continua en el punto a de ℝ si existe el límite de f(x) cuando x tienda a a y dicho límite coincide con f(a). Si no es así, la función es discontinua en el punto a.

La función anterior es continua en su dominio (ℝ) si es continua en todos los puntos de ℝ.

Ejemplos:

• Las funciones polinómicas son continuas en ℝ. Por ejemplo, f(x) = x³ - 2x² +1.

• Las funciones racionales son continuas en todo ℝ excepto en los puntos para los que se anula el denominador. Por ejemplo, f(x) = 1 / (x -1) es continua en todos los reales excepto en x = 1.

• Las funciones constantes son continuas en todo ℝ. Por ejemplo, f(x) = 3.

• La función definida por partes,

es continua para los puntos x < 2 por ser polinómica y para los puntos x > 2 por ser constante. Además, la función es continua en el punto x = 2, porque los límites laterales de f(x) cuando x tiende a 2 coinciden y son iguales a f(2). 

Intuitivamente decimos que una función es contínua cuando podemos dibujarla con un sólo trazo del lápiz, es decir, sin levantar este del papel.

EJEMPLOS DE DISCONTINUIDAD

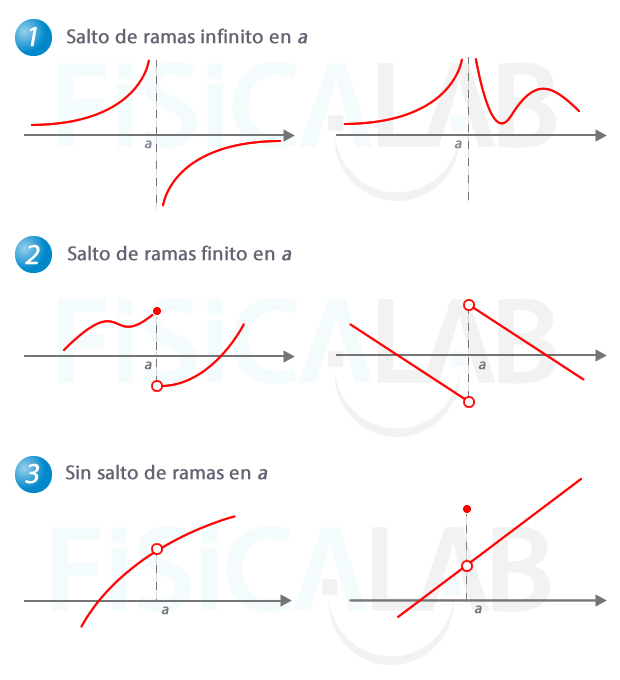
Las gráficas de la figura son discontínuas en el punto x=a, y lo son por distintas razones. 

Las gráficas de 1 presentan asíntotas verticales (ramas infinitas) en x=a.

Las de 2 presentan un salto finito en x=a. 

Las gráficas de 3 no tienen definido f(a), o, teniéndolo definido (caso de la derecha), no coincide con el valor en el entorno del mismo. En todos los casos resulta imposible dibujar las gráficas con un sólo trazo del lápiz, con lo que no son funciones continuas.

 FUNCION POR PARTES

Las funciones seccionadas, segmentadas o definidas por partes o a trozos, son funciones que se definen de un modo u otro según el valor que toma la variable $x$. Veamos un ejemplo:

Ejemplo:

$$f\left(x\right)=\{\begin{array}{cc}2x+1& \text{si}x\le 0\\ x^2& \text{si}x>0\end{array}$$

En esta función, si la variable toma un valor menor o igual que 0, la definición de la función es $2x+1$, mientras que si toma un valor positivo la definición de la función es $x^2$

${\mathrm{<br>}}^{}$

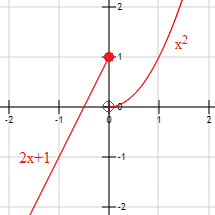
El punto sólido y el punto vacío de la gráfica indican que el valor que toma $f$ en $x=0$ es $f\left(0\right)=1$ y no $f\left(0\right)=0$ (porque $x=0$ pertenece al primer intervalo de la definición de $f$).

ASÍNTOTAS DE UNA FUNCIÓN

Una asíntota de una función (en el caso de existir esa asíntota) es una recta en el plano tal que una rama de la función f(x) que crece infinitamente en el sentido x, f(x) o en los dos sentidos a la vez, se acerca a la asíntota cada vez más. Dicho de otra manera, una asíntota es la tangente a una rama de la función en el infinito.

Tipos de asíntotas

Una función puede tener asíntotas horizontales, asíntotas verticales, o asíntotas oblicuas. Tambien hay funciones en las que no existen asíntotas (en las llamadas “ramas parabólicas”).

EJEMPLO: ASINTOTA VERTICAL.

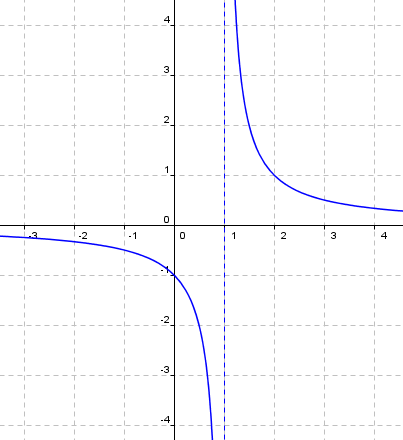
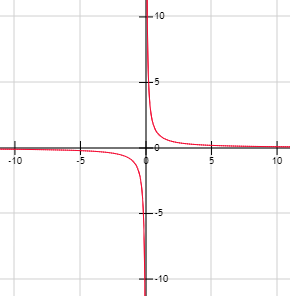
Ejemplo: ASINTOTAS VERTICAL Y HORIZONTAL

Ejemplo: ASINTOTA VERTICAL Y HORIZONTAL

La función $f\left(x\right)=1/x$ tiene asíntotas en las rectas $y=0$ y $x=0$:  

CONCEPTOS DE ANGULOS

Objetivo de aprendizaje: Identificar la medida de un ángulo en radianes (sistema cíclico), en el sistema sexagesimal y realizar conversiones entre ellos.

USO DE MEDIDAS ANGULARES

El uso de los ángulos se ha convertido en un punto de referencia para el diseño y el trabajo en nuestra vida cotidiana. Empleando en ellas distintas amplitudes, modelando nuestro mundo, transformando la ciencia e incluso torneando nuestros cuerpos para darles un mejor aspecto y cada día hacerlos más bellos. Lo anterior, por medio de las distintas medidas que intervienen al formarse, los tipos y sus características particulares, y las distintas aplicaciones que tienen; dándole un mejor aspecto al mundo y superando muchas de nuestras necesidades cotidianas. Te invitamos a conocer mucho más de las unidades de medidas angulares.

MEDIDAS DE ANGULOS

Desde la primaria estamos midiendo ángulos con el transportador; su unidad es el grado y el sistema es el sexagesimal. Sin embargo, existen otros sistemas de medida de ángulos, entre ellos están el sistema cíclico, en el cual su unidad de medida es el radian; también está el Sistema centesimal, es la unidad de medida angular, se obtiene de dividir una circunferencia en 400 partes, o bien, un recto en 100 partes, a cada parte se la denomina grado centesimal o gradian y se la simboliza con una g minúscula como índice del número, por ejemplo 30^g.(30 grados centesimales). 

    ¿CUÁLES SON LOS SISTEMAS DE MEDIDA DE ÁNGULOS?

 SISTEMA CICLICO

Un radián es la unidad de medida de un ángulo con vértice en el centro de una circunferencia y cuyos lados delimitan un arco de circunferencia que tiene la misma longitud que el radio. El radián (rad) es la unidad de medida para ángulos en el Sistema Internacional de Unidades (S.I.).



La relación del radián con la otra unidad de medida para ángulos más ampliamente utilizada, los grados sexagesimales o simplemente grados (º), es la siguiente:

1 vuelta completa de la circunferencia  =  360º  =  2 · π   radianes

Para entender la anterior igualdad, se parte de saber que la medida en radianes de un ángulo (θ) medido en una circunferencia es igual a la longitud del arco que abarca dividida entre el radio de dicha circunferencia, es decir:

	Longitud del arco
θ(radianes)  =
	Radio

Por tanto, cuando se trata del ángulo correspondiente a una circunferencia completa, cuya longitud total es  2·π·r  (siendo  r  el radio de la circunferencia) le corresponden en radianes un ángulo de:

	2·π·r
θ(circunferencia completa)  =		=  2·π  radianes
	r

En el sistema sexagesimal, el ángulo que abarca la circunferencia completa mide 360º, por lo que se puede establecer la ya vista relación entre grados y radianes:

1 vuelta completa  =  360º  =  2 · π   radianes

Otras equivalencias útiles entre grados y radianes son las siguientes:

0º = 0  rad        90º =  rad                     180º =  rad

 SISTEMA SEXAGESIMAL

El sistema sexagesimal es un sistema de unidades muy empleado cuyo fundamento es que cada unidad se divide en 60 unidades de una orden inferior, es decir, es un sistema de numeración en base 60. Se aplica en la actualidad fundamentalmente para la medida de ángulos y también en la medida del tiempo.

La unidad de medida de ángulos en el sistema sexagesimal es el grado (º), que es el resultado de dividir el ángulo llano en 180 partes iguales, o bien un ángulo recto en 90 partes, o un ángulo completo en 360 partes. A cada una de esas partes se les llama grado (º). Así, un ángulo llano mide 180º, un ángulo recto 90º y un ángulo completo 360º.

A su vez, cada grado se subdivide en otras unidades inferiores, en concreto, en sesenta partes iguales. De esta manera, cada grado se divide en 60 minutos (1º = 60´) y cada minuto, a su vez, en 60 segundos (1´ = 60´´).

•  Medidas de ángulos:  1 grado (º)  →  60 minutos (´)  →  60 segundos (´´)

•  Medidas de tiempo:  1 hora  →  60 minutos (´)  →  60 segundos (´´)

Por tanto, en general, un ángulo en el sistema sexagesimal vendrá expresado en grados, minutos y segundos, de la forma, por ejemplo: 38º 50´ 35´´ (38 grados, 50 minutos y 35 segundos). Si se omiten los minutos y segundos, por ejemplo, 45º, es porque se entiende que es 45º 0´ 0´´.

Cuando un ángulo se mide en grados, minutos y segundos, se dice que está expresado con medida compleja, mientras que si se expresa con una sola clase de unidades, se dice que es una medida incompleja o simple, por ejemplo:

32º  →  medida simple

11´´  →  medida simple

52º 17´ 45´´  →  medida compleja

4º 22´  →  medida compleja

Para sumar grados expresados en medidas complejas, primero se colocan los grados debajo de los grados, los minutos debajo de los minutos y los segundos debajo de los segundos, y se suman, como se indica en el siguiente ejemplo de la figura:

Como se ve en el ejemplo anterior, si los segundos suman más de 60, se divide dicho número entre 60; el resto serán los segundos y el cociente se añadirá a los minutos. Se hace lo mismo para los minutos, si estos resultasen también una cantidad mayor de 60.

-  Paso de una medida compleja a incompleja:

Para pasar de medidas complejas a simples  hay que transformar cada una de las unidades que tenemos en la que queremos obtener y posteriormente sumarlas, por ejemplo:

Pasar de la forma compleja  2º 25´ 30´´  a un simple en segundos:

1º)  Se pasan los 2º a minutos: 2·60 = 120 minutos, y posteriormente a segundos:

120·60 = 7200 segundos

2º)  Se pasan los 25 minutos a segundos: 25·60 = 1500 segundos

3º)  Se suman todos los segundos: 7200´´ + 1500´´ + 30´´ = 8730 ´´

Por tanto, 2º 25´ 30´´ = 8730 segundos

-  Pasar de unidades simples  a complejas:

Para pasar una medida expresada en unidades incomplejas a complejas, habrá que dividir cuando el caso sea de pasar a unidades de orden superior, o multiplicar para pasar a unidades de orden inferior, por ejemplo:



ANGULOS MAYORES QUE 360°

Nos damos cuenta que trabajar con un ángulo mayor que 360° es igual que trabajar con un ángulo  coterminal a este y menor que ese valor lo único que hay que hacer es dividir ese valor entre 360° y el cociente simboliza las vueltas que realiza pero el RESIDUO nos da el valor real del ángulo coterminal al ángulo dado.

RELACIÓN ENTRE GRADOS SEXAGESIMAL Y RADIANES

Como la medida angular de una rotación completa es de 360° 0 2 la relación entre grados y radianes está dada por la proporción:

Ésta igualdad hay que tenerla muy presente por lo siguiente 

EJEMPLOS

Se cancela la medida en grados (°) en el numerador y el denominador; luego, comienzo a simplificar cada expresión; por ejemplo, le puedo sacar la 3^ra, luego otra vez 3^ra y por último la quinta parte (recuerden que al simplificar debo sacar el mismo valor al numerados como al denominador) entonces quedara, 

DESCARGA LA ACTIVIDAD DE MEDIDA DE ANGULOS